leetcode 160 intersection of two linked lists

Posted on |

Description

Easy

2819304Add to ListShare

Write a program to find the node at which the intersection of two singly linked lists begins.

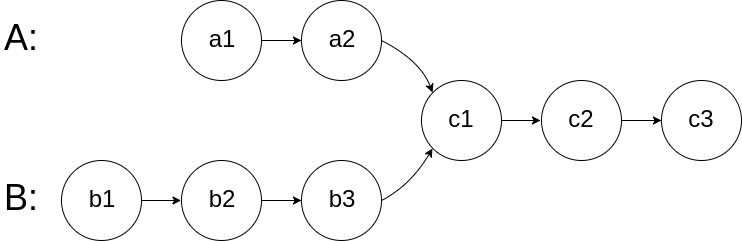
For example, the following two linked lists:

img

begin to intersect at node c1.

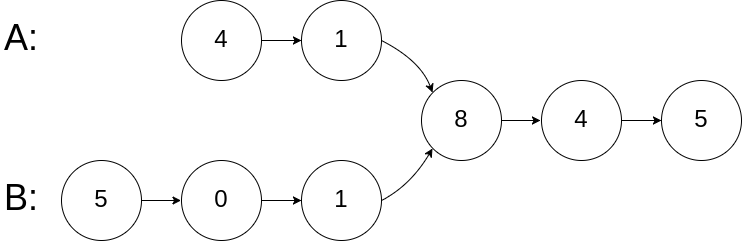
Example 1:

img

1
2
3
Input: intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3
Output: Reference of the node with value = 8
Input Explanation: The intersected node's value is 8 (note that this must not be 0 if the two lists intersect). From the head of A, it reads as [4,1,8,4,5]. From the head of B, it reads as [5,0,1,8,4,5]. There are 2 nodes before the intersected node in A; There are 3 nodes before the intersected node in B.

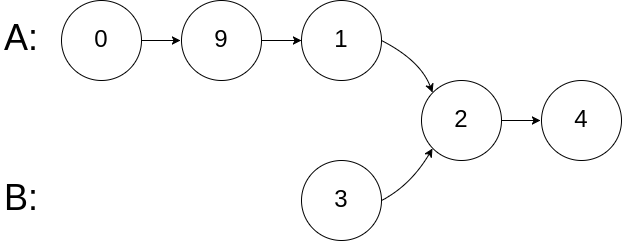
Example 2:

img

1
2
3
Input: intersectVal = 2, listA = [0,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
Output: Reference of the node with value = 2
Input Explanation: The intersected node's value is 2 (note that this must not be 0 if the two lists intersect). From the head of A, it reads as [0,9,1,2,4]. From the head of B, it reads as [3,2,4]. There are 3 nodes before the intersected node in A; There are 1 node before the intersected node in B.

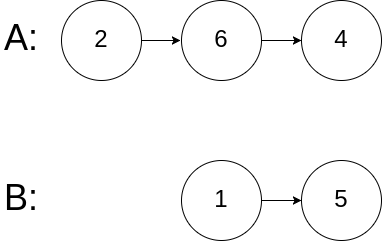
Example 3:

img

1
2
3
4
Input: intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
Output: null
Input Explanation: From the head of A, it reads as [2,6,4]. From the head of B, it reads as [1,5]. Since the two lists do not intersect, intersectVal must be 0, while skipA and skipB can be arbitrary values.
Explanation: The two lists do not intersect, so return null.

Notes:

  • If the two linked lists have no intersection at all, return null.
  • The linked lists must retain their original structure after the function returns.
  • You may assume there are no cycles anywhere in the entire linked structure.
  • Your code should preferably run in O(n) time and use only O(1) memory.

My thought

TL;DR

Basic idea is to make linkedlist A into a cycle and use Tortoise and hare algorithm to detect the circle from Linkedlist B. If B links to the circle and two pointer meets at a certain node, assign an new pointer at the head of linkedlist B and it moves 1 node per iteration. The new pointer would meet slow pointer at the entry of linkedlist B to the circle.

This problem is very typical for detecting cycle and find the entry point for a cycle in linked list, and that is why I write a post for this problem.

Problems about linkedlists always involves many technique that you would not find in problems of other type. For this problem, we could transfer it into another problems with circle detection. For a given instance, there are two condition:

  1. The given two linkedlists $A$, $B$ merges at a node $v$.

    In that situation, if we connect the tail and head of linkedlist $A$, there would be a cycle and $B$ enter the circle at node $v$.

  1. The given two linkedlists $A$,$B$ do not merge.

    We also make $A$ into a cycle, but this time, $B$ would not enter this circle.

In order to detect the existence of the circle, we use method of tortoise and hare and start at head of $B$. If the fast pointer comes to the end, then it would be the second condition, and $A$ $B$ do not merge, otherwise it would be the first condition.

After analysis above, we know it is safe to transfer original problem into the circle detection version, and what we should think next is how should we find the entry of $B$ to the circle formed by $A$.

The method to find the entry of $B$ to the circle formed by $A$ is to set a new pointer $entry$ points at head of $B$ when slow and fast pointers of tortoise and hard method meets at some nodes in circle. Then move slow pointers and pointer $entry$ by 1 node per iteration. They would merge at the circle entry. Detailed proof as below: